Waves in Paddling and Sound

           

          At my paddling race this weekend my crew would always try to catch the waves to gain an extra edge on our competition.  We would try to get the boat up to the same speed as the wave and then ride the wave until it passed us.  I began wondering how quickly we had to move the boat to get it to the same speed as the wave.  Using the equation Velocity = frequency * wavelength I could find out.  While each wave varied greatly, the waves came in about every three seconds with a wavelength of about 2.5 m.  This means the velocity of the wave was about 7.5m/s.  Unsurprisingly, this speed is well beyond the capabilities of our crew which is why the waves would ultimately pass us after a second or two.  However, the energy from the wave was transferred to our boat and helped speed us up.

            My brother joined band this year.  He is a percussionist and mainly works on drums.  I always sit on the weekends trying to do my homework through the head pounding noise and wonder how he can make so much sound.  I now know thanks to physics.

            When my brother bangs on the drums a longitudinal sound wave is generated which follows simple harmonic motion.  The sound wave then travels to my ear where I hear it.  I can also calculate the speed at which the wave travels.  The equation is: Velocity = 331 (Degrees Celsius) * Sqrt (1+(T/273 Degrees Celsius)).  The temperature was at about room level of 25 degrees Celsius.  Plugging this value in, a speed of 345.8 m/s is produced.  So, if I am standing across the room 10 m away, the sound reaches me in .0289 seconds. 

           

Floating in Physics

       

             

            As my brother and I went into our four day Thanksgiving weekend one of the first things we did was go for a swim in our pool.  As my brother and I splashed and chased each other around the pool, I began to think of the many physics concepts we had just learned.

            As I dived down under the water to the bottom of the pool I felt a large pressure on top of me.  I realized this additional pressure came from the weight of the water pushing down on top of me.  I also realized I could figure out how much greater the pressure was at the bottom of the pool using the equation P=pgh.  Density, or p, is 1000 kg/m³.  Gravity, or g, is 9.8 m/s².  The depth, or h, of our pool is approximately two meters.  Plugging these values into the pressure equation we find that the pressure at the bottom of the pool is an extra 19,600 Pascals.

            As I floated on my back I also began thinking about how much water I was displacing.  According to Archimedes’ Principle, an object in a fluid experiences an upward force equal to the weight of the fluid it displaces.  Therefore, since I was floating, I was displacing an amount of water that was equal to or just a little bit greater than my own weight.  Using the equation V = m/p I could find the volume of the water displaced.  My mass is 67.13 kg and the density of water is 1000 kg/m³.  Plugging these values in we find that I displaced .06713 m³ of water.

Riding on a Helicopter Blade

            

            As I sat at my desk trying to think of a topic for this physics blog, I became extremely irritated by the helicopter that had been buzzing over the roof of my house ever since I got back from the SAT.  Just as I was going to slam the window shut, I realized I had a topic for my blog!

            The helicopters, I presume, work for HECO and were fixing the electrical wires which run over the Ko’olau Mountains.  The basic principle of helicopters is one or more multiple large rotors which spin extremely quickly to provide the lift necessary to keep the helicopter airborne.  I wondered how quickly it took for the rotor to make a full revolution.  I then realized that with the help of Google and my new physics knowledge I could find out!

            To find out period I will use the formula T = 2(pi)r/v.  Next I need to go to Google to find out the radius and velocity of an average helicopter rotor.  I found that helicopter blades spin at a velocity below the speed of sound.  Since the speed of sound is 340 m/s we will assume that the tips of the blade spin at 330 m/s.  As there are many types of helicopters and rotor blade size can vary greatly, but from what I could see, the helicopter flying above my house was a fairly small helicopter and with some internet research I find it most likely had a rotor with a radius of about 10 meters (32 feet).  Plugging these values into the equation I find that the period is an astonishing 0.185 seconds/revolution. 

            Next I began to wonder, similar to Einstein’s famous thought experiment with a beam of light, what it would be like to ride on the tip of a helicopter blade.  What centripetal force would I experience?  Using the equation F_c = mv²/r I can find out.  My mass is approximately 65.8 kg and I already know the velocity and radius.  If I were riding on the tip of a helicopter blade I would experience a centripetal force of 76,0648 N.  Force comparison, it takes 4,000 N to break the femur bone which is one of our strongest bones since it is meant to support our body.

Soccer Momentum and Collisions

            I was playing a pickup game of soccer at the park in my neighborhood earlier today.  In the second half of the game a player from the other team was passed the ball and broke away down field toward my team’s goal.  I followed in hot pursuit, sprinting to try and catch up.  Unfortunately, the opponent who I was chasing stumbled and fell, I couldn’t stop in time and I was then catapulted into him.  Luckily, we were both alright, but how come I couldn’t stop in time?  I began thinking about what I had learned in physics and I realized it was due to momentum.

            Using the equation p=mv we can roughly estimate my momentum immediately before the collision.  I have a mass of 65.77 kg and I was most likely running at around 7 m/s.  Using these values we find that I have a momentum of 460.39 N s.  So how much force would I have had to use in order to stop in time and avoid the collision? 

            Using the equation F=(mv)/t we can calculate the hypothetical force needed to stop.  My mass is constant at 65.77 kg.  The change in velocity is 7/ms since I will need to decelerate to a complete stop to avoid the collision.  We will then have to estimate the change in time to be around a quarter of a second as I was running directly behind my opponent and I was slowed by reaction time as well.  Plugging these values back into the original equation, we find that the force needed to stop completely would have been 1841.56 J.  Unluckily, I was not able to meet the force required to stop and collided with my opponent.  However, what type of collision did I have?

            To find out what type of collision I was involved in, we must look at whether Kinetic Energy was conserved and whether my opponent and I stuck together or bounced off one another.  Kinetic energy was definitely not conserved during the collision as my opponent slightly sped up when I hit him, but I slowed down a great deal.  Energy was also lost due to friction and other non-conservative forces.  My opponent also stuck together after the collision.  Using this information we can find that I was involved in an inelastic collision.

                       

Physics at the Circus

         

            This weekend I went to Cirque du Soleil at the Neal Blaisdell center.  Besides being a remarkable spectacle to watch, the circus has an unbelievable amount of physics involved.  From the high flying trapeze artists to the acrobats dangling from pieces of red cloth and the gymnasts climbing vertically up four story ropes, almost every aspect of the circus was relatable to concepts I have learned in physics. 

            Work was done throughout the performance.  Anytime an acrobat started running from a dead stop a change in kinetic energy (KE) resulted and thus we know work was done.  We know this because we observed that their velocity increased and thus their kinetic energy must increase as well since kinetic energy is equal to 1/2mv².  Anytime an acrobat started climbing vertically up a rope a change in potential energy occurred so we know work was done as well.  We know a change in PE occurred because PE = mgh and the performers gained height as they climbed the ropes.

            However, once the rope climbers reached the top of their rope it would seem that they would be in quite a predicament since PE_i +KE_i = PE_f +KE_f.  So, theoretically all of the PE they had just gained by climbing would be converted back into KE as they descended the rope, which would not be a good thing for the acrobats.  However, the acrobats can rely on Non-Conservative forces (forces that decrease the mechanical energy of a system) such as the friction between their hands and the rope to slow their descent and reduce their KE as they descend allowing for a safe landing.

            Perhaps the best examples of the equation PE_i +KE_i = PE_f +KE_f were the trapeze artists.  Their wide parabolic arcs across the stage constantly converted PE to KE and vice versa.  At the top of their arc, the trapeze artists have no KE and are all PE.  At the bottom of their arc, the trapeze artists have no PE and have all KE.  In addition, the trapeze artists most likely had the most power in the show.  Power is defined as change in energy divided by change in time.  Since the trapeze artists went through large energy changes in short amounts of time through their parabolic arcs, I believe they had the most power out of all the performers.

Guinea Pigs on an Inclined Plane!

Last Christmas my family acquired two new members, Arthur and Cinderella.  Arthur and Cinderella are two guinea pigs that my brother and I adopted from the Hawaii Humane Society.  Since it’s been almost a year since we got our two furry friends, I decided that in my building technologies class I am going to build a large guinea pig sized house for the guinea pigs to sleep and play in when they are in their outdoor cage.  One of the hardest problems I’m struggling with when designing the guinea pig house is how steep I should make the ramps from one floor of the house to another.  I want to make the ramps as steep as comfortably possible in order to minimize the amount of space the ramps take up, however, I don’t want to make the ramps too steep or the guinea pigs won’t be able to climb them!

In order to help find out the optimal ramp angle, I thought about the lessons I learned in physics and how to find the effect of gravity on an object on an inclined plane.  Although I don’t know the exact strength of my guinea pigs I figure that having the guinea pigs overcome a force that is approximately 50-60% of their body weight would be comfortable for them.  I also need to factor into account the length of each ramp possibility.

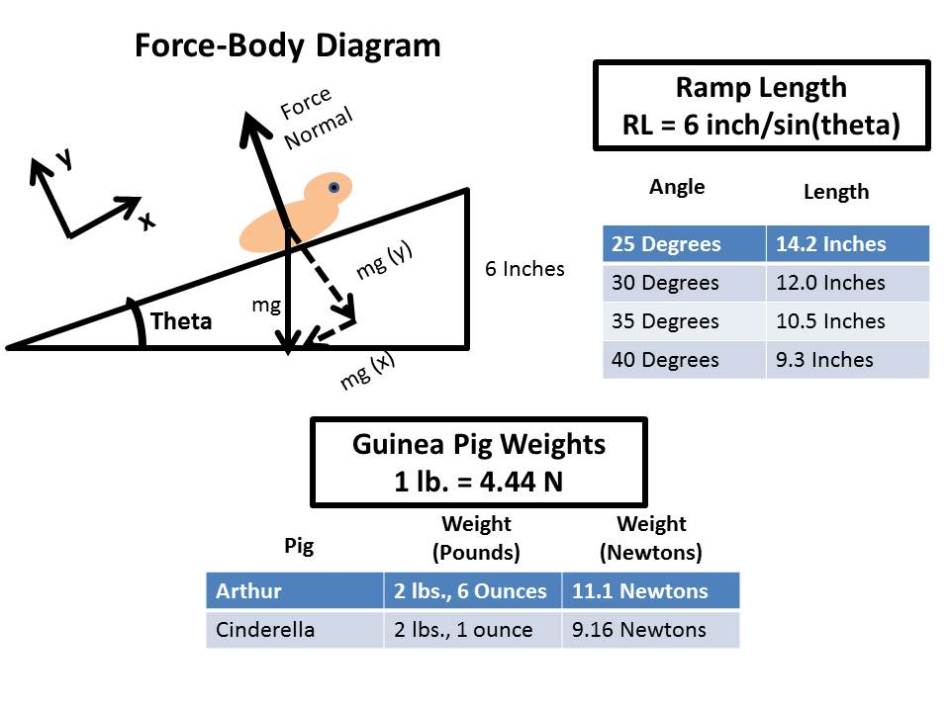
To start off, I weighed both of the guinea pigs.  Arthur came out to two pounds and eight ounces.  Cinderella weighed two pounds and one ounce.  Using the conversion of one pound = 4.44 Newtons, their weights come out to 11.1 N and 9.16 N respectively.  Using these weights I set out to find the effect gravity would have on the guinea pigs at different ramp angles.

To start off I drew a Force-Body Diagram which showed the guinea pigs on a ramp.  I then drew in the force normal as well as mg, mg_x, and mg_y.  Unfortunately, I couldn’t devise a way to accurately measure the guinea pig’s coefficients of friction since there were too many uncontrollable variables, the main one being the guinea pig’s force.   As a result I have to assume the guinea pig is on a frictionless surface.

The next step I completed was to determine which ramp angles I wished to experiment with.  I knew that the height in-between each floor would be six inches, so I could then calculate ramp length using: Ramp Length = six inches/sin(theta).   Using guess and check I found that angles between 25 degrees and 40 degrees would give me an optimal ramp length between 14.2 inches and 9.3 inches.

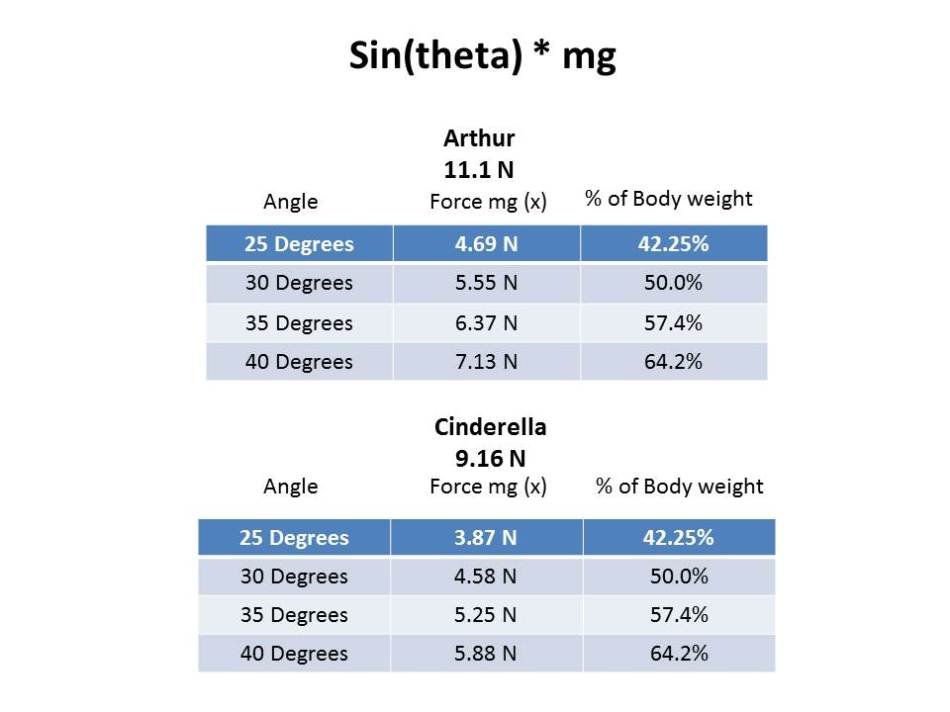
After finding the optimal ramp angle range based of ramp length, I set out to find the optimal ramp angle range based off of the force mg_x.  I don’t need to account for mg_y because mg_y decreases as angle increases so I don’t have to worry about force mg_y being too large for the guinea pigs to handle.  Therefore all I have to do is compute mg_x at the different angles and find what percent of the guinea pig’s weight mg_x is.  Angles that produce an mg_x that is less than 60% of the guinea pig’s bodyweight will be considered optimal.  The optimal angles based off of mg_x will then be cross-examined with the optimal angles based off of ramp length to find the overall best angle.

To compute mg_x I have to find sin(theta) and then multiply by mg or the pig’s weight.  Since Arthur and Cinderella have different weights they will have different mg_x forces so each must be computed separately.  However, the % of body weight will be the same for both Arthur and Cinderella since mg and mg_x are proportional.

After comparing the effect of each angle on ramp length and forces on each guinea pig, I have decided that the best angle to use during the construction of the ramps in the guinea pig cage, will be 35 degrees.  By using an angle of 35 degrees I will be able to use a fairly short ramp of only 10.5 inches while only creating a force in the x direction that is 57.4% of the guinea pig’s weight which should be a reasonable force for the guinea pigs to handle.

Kayaking: Current and Vectors

Once again, it was through kayaking this Saturday that I found more real-world applications of physics concepts.  I began to think about my kayak’s movement in relation to current.  Similar to the boat simulations we have been doing in class, the kayak’s movement and direction is greatly affected by the current of the water.  The Ala Wai canal current is unusual because there is a current going both vertically, up and down the canal and horizontally, left to right across the canal.  It is much easier to feel the effects of the up and down current, as I felt myself moving much more quickly and with less effort down the canal, while paddling up the canal against the current required more effort.

The horizontal current flowing across the canal left to right is more difficult to deal with in the kayak.  I had to make adjustments in my direction to stay on course and travel in a straight line.   Using an average vertical speed for the kayak of 2 m/s and an average current speed of .1 m/s I can calculate the angle change I need to make to travel in a straight line.  With a vertical vector of 2 m/s heading South and a horizontal vector of .1 m/s heading East a right triangle can be formed.  The hypotenuse of the triangle is my actual speed I am traveling at, the angle of the triangle is the directional angle I must be traveling in, in order to maintain a straight line path.  Using the Pythagorean theorem, a²+b²=c², the hypotenuse can be calculated: .1²+2² = 2.002²  The actual speed I am traveling at is therefore 2.0155 m/s.  The direction I am traveling at can be found by taking the tan^-1 of the right triangle.  Tan^-1(.1/2) = 2.86 Degrees West of South.  While the effect of the current may not seem large, causing only minute changes in direction, over the course of a race it can have quite a large effect and if it is not adjusted for, the current can move a kayaker far off course.  Using physics though, a kayaker can adjust for current and travel in a straight path to the finish line.

Kayaking Physics: Displacement, Acceleration, and Kinematics

During my kayaking practice on Saturday, in the ‘pristine’ waters of the Ala Wai Canal, I began to see some physics concepts that applied to the real world.  I first noticed that the kayak racing course, similar to the metaphorical running track we discussed in class, was shaped like an oval.  Kayakers will start along a straightaway and then make a 180 degree turn and come back along a straight away.  I then realized how whoever is coming out of the 180 degree turn, regardless of what place they are in, will have the greatest displacement on the course at that moment. 

I also began to think about how acceleration and velocity factor into a kayaking race.  We did a few practice races and I found myself accelerating more slowly than some of my teammates, choosing to conserve my energy over the long distance race.  However, I began to realize that using my energy to accelerate quickly could actually give me an advantage.  Using the kinematic equation: (Displacement) = ½(Velocity_initial + Velocity_Final)(Time); I could calculate how best to start my races.  For example, if I took five seconds to reach  a top speed of about 2.5 m/s in the kayak I would travel 6.25 meters from the start line.  However, if I put in some extra energy and accelerated to the top speed of 2.5 m/s in four or even three seconds (assuming I maintained the top speed after acceleration), I would travel 7.5 meters or 8.75 meters after five seconds.  Accelerating to top speed just one second quicker would give me an extra 1.25 meters of distance, a little over half a boat length, which in turn would give me better position in the race and could help me in the long term.  Using physics I realized that accelerating quickly off the start line could give me a considerable advantage in a kayaking race with only a little extra energy expenditure.

Hello world!

Welcome to WordPress.com! This is your very first post. Click the Edit link to modify or delete it, or start a new post. If you like, use this post to tell readers why you started this blog and what you plan to do with it.

Happy blogging!